Sodium hydroxide Formula - Sodium Hydroxide Uses, Properties, Structure and Formula

Sodium hydroxide is one of the most common inorganic bases or alkalis. It is also called caustic soda or lye.

Formula and structure: The chemical formula of sodium hydroxide is NaOH, and its molar mass is 40.01 g/mol. It is the alkali salt of sodium, and its structure is shown below:

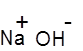
It is an ionic compound consisting of sodium cation (Na⁺) and hydroxide (OH^-) anion.

Preparation: Sodium hydroxide is industrially produced using the electrolytic chloralkali process, in which electrolysis of aqueous sodium chloride solution gives chlorine gas and sodium hydroxide. NaOH is obtained as a 50% solution in water, and then dried to give solid sodium hydroxide flakes or pellets.

2 NaCl + 2 H₂O → 2 NaOH + Cl₂ + H₂

Physical properties: It is an odorless, white crystalline solid with a density of 2.13 g/mL, and melting point of 318 °C. It is widely available as pellets, flakes, granules, and also as aqueous solutions of different concentrations.

Chemical properties: Sodium hydroxide is soluble in polar solvents such as water, ethanol, and methanol, and insoluble in organic solvents. Dissolving solid NaOH in water is a highly exothermic reaction and the resulting aq. NaOH solution is a colorless, odorless and important base used in the laboratory. As a strong base, sodium hydroxide readily reacts with acids such as HCl, to form the corresponding salts, as shown below:

NaOH + HCl → NaCl + H₂O

Sodium hydroxide is very hygroscopic (absorbs water from air) and also absorbs carbon dioxide from air.

Uses: Sodium hydroxide is one of the most widely used bases in industry. Its main uses are in the paper industry, petroleum industry, textiles industry, in the manufacture of soaps and detergents, in the Bayer process of aluminum production, industrial cleaning, and for pH regulation. It is also used in the food industry for many applications.

Health effects/safety hazards: It is a strong and highly corrosive alkali, which readily decomposes living tissues. Skin contact of NaOH solutions can result in severe chemical burns, and eye contact can cause permanent blindness. Solid NaOH reacts with water and acids in a very exothermic reaction, and can cause burns through splashing.