Dinitrogen Tetroxide Formula

Dinitrogen tetroxide, also known as nitrogen tetroxide, is a inorganic compound used as reagent in synthesis of different compounds.

Formula and structure: Dinitrogen tetroxide chemical formula is N₂O₄ and the molar mass is 92.01 g mol^-1. The structure of the oxide is formed by two -NO₂joined by one single bond in a planar structure. Its chemical structure can be written as below, in the common representations used for organic molecules.

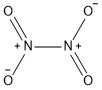
Occurrence: Dinitrogen tetroxide is not found in nature.

Preparation: Dinitrogen tetroxide is prepared in laboratories to be used as reagent in reactions. It is prepared from ammonia that is oxidized to nitric oxide, which is in sequence oxidized to nitrogen dioxide:

4 NH₃ + 5 O₂ → 4 NO + 6 H₂O

2 NO + O₂ → 2 NO₂

Nitrogen dioxide which is then dimerized into nitrogen tetroxide:

2 NO₂ ⇌ N₂O₄

A second method is the reaction of nitric acid and metallic copper.

2 HNO₃ → N₂O₄

Physical properties: Dinitrogen tetroxide is a colorless liquid in equilibrium with an orange gas. Its density is 1.44 g mL^-1. The melting point of the compound is -11.2 °C, the boiling point is 21.69 °C and above this temperature, it decomposes to NO₂. Dinitrogen tetroxide is not soluble in water, when adding to water, it reacts to form nitric acid and nitrous acid.

Chemical properties: Dinitrogen tetroxide keeps an equilibrium with nitrogen dioxide, through the reaction:

N₂O₄ ⇌ 2 NO₂

This equilibrium breaks irreversible the N-N bond in dinitrogen tetroxide, originating the single molecule NO₂.

One of the main uses of dinitrogen tetroxide is the production of nitrous and nitric acid, by the reaction of it in water:

N₂O₄ + H₂O → HNO₂ + HNO₃

Uses: Dinitrogen tetroxide is used as rocket propellant. Its physical state of liquid makes it ideal to be used as propellant where it is mixed with another nitrogen compound, hydrazine. Dinitrogen tetroxide is also used as reagent in some reactions due to it is a great oxidizer.

Health effects / safety hazards: Dinitrogen tetroxide is noxious for health. It can cause headache, nausea, difficulty in breathing, lethargy and rapid pulse. If the exposure continues, it can also cause asphyxiation and pulmonary edema. At high temperature, it decomposes to NOx gases and can react with wood and other combustibles. It can react with reducing materials.