Boric acid Formula - Boric Acid Uses, Properties, Structure and Formula
Boric acid is a weak inorganic acid with antiseptic properties, and is also called boracic acid or orthoboric acid.
Formula and structure: The chemical formula of boric acid is H3BO3 (or B(OH)3). Its molecular formula is BH3O3, and its molar mass is 61.83 g/mol. The chemical structure of boric acid is shown below:
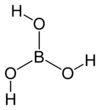
The central boron atom is connected to three hydroxyl (-OH) groups, which are capable of strong hydrogen bonding. Its solid crystalline structure consists of parallel layers of boric acid held together in place by hydrogen bonds.
Occurrence: Boric acid occurs naturally in volcanic areas, and in certain minerals such as borax (as sassolite). It is also found in sea water, plants, and fruits in small amounts.
Preparation: Boric acid is prepared by reacting minerals such as borax (Na2B4O7·10H2O), with strong acids like HCl:
Na2B4O7·10H2O + 2 HCl → 4 H3BO3 + 2 NaCl + 5 H2O
It can also be prepared by the hydrolysis of boron trihalides (such as BBr3) or diborane (B2H6):
BBr3 + 3 H2O → B(OH)3 + 3 HBr
B2H6 + 6 H2O → 2 B(OH)3 + 6 H2
Physical properties: Boric acid is a white crystalline solid with a density of 1.435 g/mL, melting point of 170.9 °C and boiling point of 300 °C.
Chemical properties: Boric acid is a weak monobasic acid, and is considered a Lewis acid. It dissolves in boiling water and in anhydrous sulfuric acid. When heated to high temperatures (over 170 °C), it undergoes dehydration to form metaboric acid (HBO2):
H3BO3 → HBO2 + H2O
Uses: Boric acid is non-toxic with antibacterial properties, and it is mainly used as an antiseptic agent, acne treatment, preservative, insecticide, pH buffer, swimming pool chemical, flame retardant, and a precursor to many useful chemicals. It is used industrially for the manufacture of fiberglass, household glass products and the glass used in LCD displays.
Health hazards/ health effects: Low concentrations of boric acid does not pose any toxicity. However, boric acid is poisonous if swallowed or inhaled in large quantities. High concentrations of boric acid can potentially lead to reproductive problems. Exposure to boric acid over long periods of time can cause possible kidney damage.
|
Related Links: |
