The Binary Number

We typically work in base 10. So our numbers are made up of 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. However, computers typically run on the binary system. The binary number system, or base 2, works with just 0 and 1.
Converting from Base 2 (Binary Numbers) to Base 10:
Your first question might be... How do we show numbers like 2, 3, 4, etc. if there are only 1s and 0s. Before we look at converting, let's look at what a number in binary code might mean to further understand.
First, you need to realize that each place value represents a power of 2.
__________ __________ __________ ___________ __________ __________
25 24 23 22 21 20
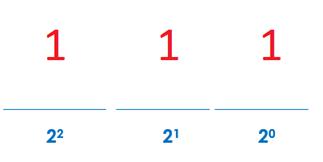
So the number 1112 would represent 1 x 22 + 1 x 21 + 1 x 20 = 4 + 2 + 1 = 7 in base ten.
How did we do that? We just multiplied each number times its corresponding power of 2 position.
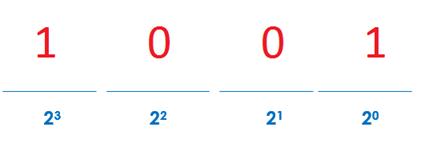
Here is another example: 10012
1 x 23 + 0 x 22 + 0 x 21 + 1 x 20 = 8 + 0 + 0 + 1 = 9
Converting from base 10 to base 2:
To write 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13... in base 2 we would have....
1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, ...
But what if you want to convert other base ten numbers to base 2?
Example: 34
1. Step 1: Determine the largest power of 2 that could divide into the given number.
You might want to start by making a list of powers of 2.
Powers of 2
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048,...
Notice that 32 is the largest power of 2 that could be part of 34.
2. Rewrite 34 as a sum of powers of 2.
So 34 becomes 32 + 2 or 25 + 21.
3. Now place 1s in the positions for the powers of two that you used and 0s for any powers that were not used.

4. So 34 in base 10 is equal to 100010 in base 2.
We can show that 100010 is meant to represent 34 by adding a subscript to the right. The small 2 shows that we used the binary system or base 2.
34 = 1000102
Example: 237You might want to start by making a list of powers of 2.
Powers of 2
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048,...
Notice that 32 is the largest power of 2 that could be part of 34.
2. Rewrite 34 as a sum of powers of 2.
So 34 becomes 32 + 2 or 25 + 21.
3. Now place 1s in the positions for the powers of two that you used and 0s for any powers that were not used.

4. So 34 in base 10 is equal to 100010 in base 2.
We can show that 100010 is meant to represent 34 by adding a subscript to the right. The small 2 shows that we used the binary system or base 2.
Start by determining how to break this number down into powers of 2.
237 = 128 + 64 + 32 + 8 + 4 + 1
Now we will rewrite it using powers of 2.
237 = 27 + 26 + 25 + 23 + 22 + 20
Finally, we will rewrite the number using 0s and 1s.
237 = 111011012
Let's Review:
The Binary Number System, which can also be called the Base 2 Number System is a way of writing numbers using 0s and 1s. Converting from either base 2 to base 10 or base 10 to base 2 requires the use of powers of 2 instead of powers of 10.
Related Links:
Math
algebra
To link to this The Binary Number page, copy the following code to your site:
