Subtracting Fractions with Unlike Denominators
Let's look at a model to help us see what is happening.

Minus
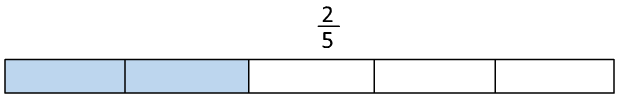
Right now it is difficult to take two-fifths away from three-fourths because the parts are not the same size. So our first job is to rewrite the problem so that both fractions have equal sized pieces.
We will change each fraction to have 20 total pieces (the smallest multiple that 4 and 5 have in common.

Minus
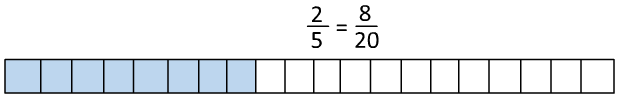
Now we can see that there would be a section left over when we take away
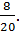
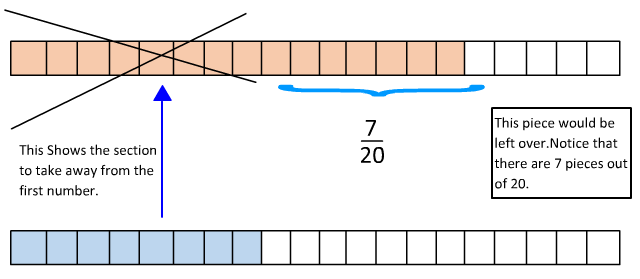
So we can see in the model that
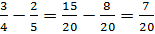
Hopefully the model helped you to visualize the steps. However, drawing a model can be very time consuming, so we can carry out these same steps without one.
Step 1: Choose a common denominator by calculating the least common multiple of the two denominators.
Step 2: Rewrite the fractions using the common denominator.
Step 3: Subtract the numerators and keep the denominators the same.
Let's try the steps in a few examples.
Example #1:
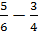
Step 1:
4, 8, 12, 16, 20, 24, 28, 32, ....
6, 12, 18, 24, 30, 36, 42, 48,....
The least common multiple of 6 and 4 is 12.
Step 2:
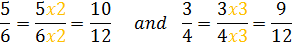
Step 3:
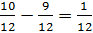
So we can see that
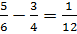 .
.Example #2:
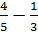
Step 1:
5, 10, 15, 20, 25, 30,....
3, 6, 9, 12, 15, 18, 21,....
So the least common multiple is 15.
Step 2:
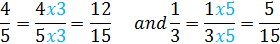
Step 3:
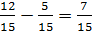
Therefore,
Let's Review:
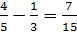
When subtracting fractions with unlike denominators, it is important to first get common denominators. Then subtract the numerators and keep the denominator the same.
Related Links:
Math
Fractions
Fraction Subtraction Worksheets
Fractions Subtraction Game
Add and Subtract Like Fractions Quiz
Add and Subtract unlike fractions Quiz
Compare & Order Fractions Quiz
Factors
