Sometimes we make an estimate or a guess and then later find out that we were a little off. We can calculate just how much we were off using percent error.

Here is the formula we use for determining the percent error:

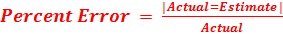x 100

Example 1:

Hillary estimated that there were about 130 shoppers at her store today. However, there were actually 135. What is her percent error?


Now we are ready to determine the percent error.



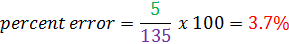
Example 2:

Carlos guesses that he has been running for 38 minutes. He has actually only been running for 32 minutes. Determine his percent error.



(The difference should always be a positive amount.)



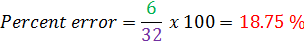
Example 3:

Sunil measured the piece of wood to be 14 cm long. It was actually 17 cm long. What is the percent error?





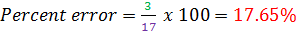
Example 4:

Susan estimated that the coin would land on heads 400 times. It actually landed on heads 320 times. Determine the percent error.





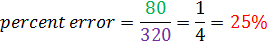
So why is percent error important?

Mathematicians and scientists like to find out if the theoretical ideas are close to the actual results. They can use the percent error to help determine the relationship between what actually happened and what they expected to happen.



Related Links:
Math
Fractions
Factors