One Step Equations
Adding and Subtracting:
If I add 3 and then subtract 3, I end up with the number I started with.
5 + 3 - 3 = 5
Multiplying and Dividing:
If I multiply by 3 and then divide by 3, I end up with the number I started with.
5 x 3 ÷ 3 = 5
Inverse operations are a key point to solving an equation and figuring out the value of the variable. Recall that a variable is used in place of an unknown number. When we have an equation, with an equal sign, we can solve for the variable.
Examples:
1.) x + 5 = 19
There are lots of ways to think about this question. To start to get an idea, let's draw a model.
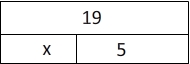
So we are basically asking, "What could I add to 5 to get to 19". To find out, we use the inverse operation. 19 - 5 = x
So it follows that x must be 14. Let's add it to our model and see if it works.
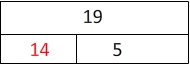
Now we have 14 + 5 = 19, which is a true statement.
Drawing a model for every example can become tedious. So instead, we will show our steps algebraically.
x + 5 = 19
x + 5 - 5 = 19 - 5We will undo the addition, by subtracting. Be sure to use the inverse on both sides of the equal sign.
x = 14
2.) x - 4.2 = 23.7
x - 4.2 + 4.2 = 23.7 + 4.2Here, we started with a subtraction statement, so we will use addition as the inverse operation to "undo" the subtraction and get the variable alone.There are lots of ways to think about this question. To start to get an idea, let's draw a model.
So we are basically asking, "What could I add to 5 to get to 19". To find out, we use the inverse operation. 19 - 5 = x
So it follows that x must be 14. Let's add it to our model and see if it works.
Now we have 14 + 5 = 19, which is a true statement.
Drawing a model for every example can become tedious. So instead, we will show our steps algebraically.
x + 5 = 19
x + 5 - 5 = 19 - 5We will undo the addition, by subtracting. Be sure to use the inverse on both sides of the equal sign.
x = 14
2.) x - 4.2 = 23.7
3.) 6y = 54
6y ÷ 6 = 54 ÷ 6We can do the same thing when faced with questions that involve multiplication and division.
y = 9
As you continue to learn more mathematics, you will start to see division shown as a fraction. This same solution could have been shown this way:
6y = 54
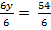Here, we have used the fraction bar instead of the division symbol, and still ended in the same solution.
y = 9
4.)
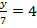In this question, the fraction shows that y was divided by 7. So something divided by 7 resulted in 4. To find the answer, we will use the inverse of division.
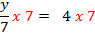
y = 28Does our answer make sense? Yes,I can replace the y with a 28 and solve.
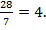
Let's review:6y ÷ 6 = 54 ÷ 6We can do the same thing when faced with questions that involve multiplication and division.
y = 9
As you continue to learn more mathematics, you will start to see division shown as a fraction. This same solution could have been shown this way:
6y = 54
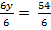Here, we have used the fraction bar instead of the division symbol, and still ended in the same solution.y = 9
4.)
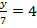In this question, the fraction shows that y was divided by 7. So something divided by 7 resulted in 4. To find the answer, we will use the inverse of division.
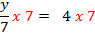
y = 28Does our answer make sense? Yes,I can replace the y with a 28 and solve.
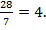
When solving a one-step equation, we can use the inverse operation to get the variable by itself. Just be sure to perform the same operation on both sides of the equal sign in the equation.
Related Links:
Math
Fractions
Factors