Factors
Example: 4 x 7 = 28
4 and 7 are factors of 28.
You could also multiply 2 x 14 or 1 x 28. These are all factors of 28.
Let's list out the factors of 28: 1, 2, 4, 7, 14, 28. Each of the numbers in this list are factor pairs.
We can move from the outsides to the center and pair the numbers together to make sets of numbers that will multiply to make 28.

Take a look at another example:
List all the factors of 60.
Whenever we are asked to list out all of the factors, we can use these factor pairs to help make sure that we have not missed any. We will start on the outside and work our way in.
The first pair is 1 and 60.

Next, we will divide 60 by 2 because 60 is even. So the second pair is 2 and 30.

From here, we can continue to try the next number up in order. So the third pair is 3 and 20.

Now we will use 4 and 15.

60 ends in a zero, so we can use 5 and 12.
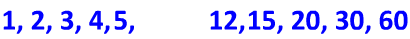
Then we will add 6 and 10.
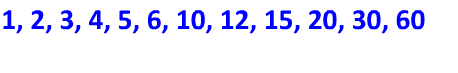
Now, in between 6 and 10 is 7, 8 and 9. Once we have checked if any of these three numbers will go into 60, we know that we have found all of the factors of 60. None of them will divide evenly into 60. Therefore we have all of the factors of 60 listed above.
Factors are important because they help us solve problems. Factors can help us be able to break things into groups.
Example: There are 24 people in a room together at a party. Everyone would like to take part in games during the party. What size groups can we break the people into so that no one is left out and everyone can play?
To solve this problem, we need to know the factors of 24.
List them out: 1, 2, 3, 4, 6, 8, 12, 24
Let's see how the factor pairs can help us.
-The first pair, 1 and 24, doesn't tell us much. It just means that we could have 1 group of 24.
-The second pair tells us we could have 2 groups of 12 or 12 groups of 2.
-The third pair tells us we could have 3 groups of 8 or 8 groups of 3.
-The fourth pair tells us we could have 4 groups of 6 or 6 groups of 4. Now we can see that there are several possibilities for grouping the party guests.
Let's check out a more geometrical example.
Example: Xin has a plot of land with an area of 36ft2. He wants to break his plot of land into different equal sized sections to plant different vegetables. How many vegetables can he plant?
Again, we will start by listing out the factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Let's again see how the factor pairs can help us.
The first pair, 1 and 36, doesn't tell us much. It just means that we could have 1 vegetable taking up all of the land or 36 vegetables taking up 1 square foot.
The second pair tells us we could have 2 veggies using 18 square feet each or 18 veggies using 2 square feet each.
The third pair tells us we could have 3 veggie using 12 square feet each or 12 veggies using 3 square feet each.
The fourth pair tells us we could have 4 veggies using 9 square feet each or 9 veggies using 4 square feet each.
The last pair tells us that we could have 6 veggies that each take up 6 square feet.
Each of these are possible solutions. And now Xin can decide how many plants to get.
Let's Review:
Factors are numbers that can be multiplied together to make another number. So 3 and 7 are factors of 21.
We can use factors to help us solve problems that ask us to break something into equal groups or equal sized sections.
Related Links:
Math
Fractions
Factors
