Imagine that you have 5 songs randomly playing on your MP3 player all from the same album. What is the probability that the 5 songs will play in the same order as they did appear on the album?

Let's first determine how many different ways the songs could play.

There are 5 choices of songs that could play first. 5

One of them plays. So now there are 4 choices for the second song.4

Another song plays. Now there are 3 choices for the third song.3

And another plays. Now there are 2 choices left.2

And then there is one song left for the last play.1

So there are 5 x 4 x 3 x 2 x 1 = 120 different ways that the songs could play. We write this as 5!.

We read this as 5 factorial.

That means that there is a 1 in 120 chance that the songs will play in the same order as they are on the album.

Now what if there were 6 songs?

We would need to first solve 6! Or 6 factorial.

6! = 6 x 5 x 4 x 3 x 2 x 1 = 720 different ways to play the six song.

So the probability of the songs being in order is 1 out of 720.

We can also simplify expressions with factorials.

Example:

First, let's look at what this means.

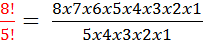
Next, we will cancel out the common factors.

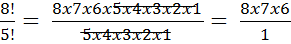= 336

Let's try another.

Example:

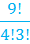
First, we will rewrite the problem.

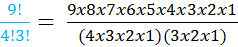
Then we can start to cancel common factors again.



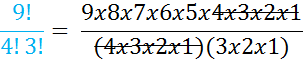
We can further simplify.



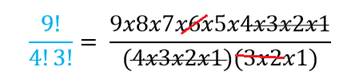
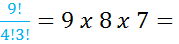= 504

One important thing to remember is that just like x⁰ = 1, 0! = 1 also.

In summary....

Factorials are just a special way to show a product. We use them in permutations and combinations to help determine probabilities. If you are asked to solve an expression with a factorial, you need to multiply the whole numbers from the given number down to one.

5! = 5 x 4 x 3 x 2 x 1

4! = 4 x 3 x 2 x 1

3! = 3 x 2 x 1

2! = 2 x 1


Related Links:
Math
Fractions
Factors