Expanded Notation
There are basically two acceptable ways to show numbers in expanded notation. Here are some examples.
Example: 4,981
Method #1: 4,000 + 900 + 80 + 1
In this method, we can see that 4 is in the thousands place because we have rewritten it as 4,000. The 9 is in the hundreds place, so we wrote it as 900.
To write a number in the form, you just replace all the numbers that came after the digit with zeros.
Here is another example using method 1.
Example: 15,807
Method #1:: 10,000 + 5,000 + 800 + 7
Again, we can see the place value of each digit in the number. Notice that there were no tens in this number.
The second method takes the work from method #1 a step further.
Example: 4,981
4,000 + 900 + 80 + 1
Method 2: (4 x 1,000) + (9 x 100) + (8 x 10) + (1 x 1)
This method shows the place value as a power of ten. We could have even taken this another step and used exponents to show the powers of ten.
The answer would now be: (4 x 103) + (9 x 102) + (8 x 101) + (1 x 100)
Example: 15,807
10,000 + 5,000 + 800 + 7
Method 2: (1 x 10,000) + (5 x 1,000) + (8 x 100) + (7 x 1)
Expanded Notation with Decimals
Using the powers of ten, we can also write numbers with decimals in expanded notation.
Example: 89.34
We will start by using the first method. This will help us build to method #2.
80 + 9 + 0.3 + 0.04
(8x 10) + (9 x 1) + (3 x
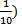+ (4 x 
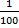)The expanded notation helps us to see that the 3 is in the tenths place and the 4 is in the hundredths place.
Example: 713.052
700 + 10 + 3 + 0.05 + 0.002
(7 x 100) + (1 x 10) + (3 x 1) + (5 x
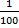) + (2 x 
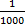)You might note that the number of zeros in the denominator for the decimals is the same as the number of places from the decimal point to that digit. For example, the 2 is three digits from the decimal point, so there are three zeros in the denominator.
Writing the numbers this way helps us to see that the 5 is in the 100ths places and the 2 is in the 1,000ths place.
Related Links:
Math
Fractions
Factors