How would you add

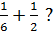
Let's look at a visual example of the two fractions



Right now, it is difficult to add these together because they are different sizes. But a little change in the way that we look at ½ can help to make this question a little easier!

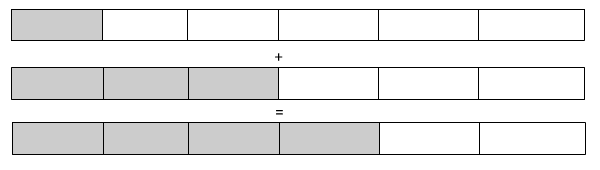
Imagine that the second fraction has 6 pieces, like the first fraction. We would still shade in half the squares to model ½.



Becomes



Now, let's try to add them together.



So we can determine that

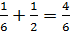
Drawing a picture, like in the previous example, can be quite tedious and not a convenient way to solve. So let's determine what is happening mathematically.

Step #1: We need to get common denominators. (This is why we changed the second diagram to be out of 6.)

Step #2: What ever we do to the denominator, we have to do to the numerator. (The 2 on the bottom became 6 using 2 x 3 = 6. So the top became a 3 because 1 x 3 = 3).

Step #3: Add the rewritten fractions together.

Let's see the steps in action.

Example #1:

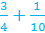
Step 1: Determine the common denominator.

Think about multiples 4, 8, 12, 16, 20, 24, 28, 32,.... Or 10, 20, 30, 40,....

They both have 20 in common.

Step 2: Now change the numerators.

4 x 5 is 20, so we need to multiply the top by 5 as well.



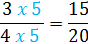
10 x 2 = 20, so we need to multiply the top of the second fraction by 2 as well.



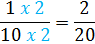
Step 3:   



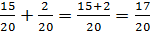
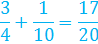
Example #2:

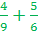
Step 1: 6 and 9 have a common multiple of 18

6, 12, 18, 24, 30, 36,....

9, 18, 27, 36, 45, 54,....

Step 2: Rewrite the fractions with the common denominators.





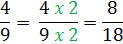
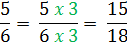
Step 3: Add.



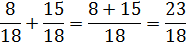
The answer is an improper fraction. You can leave your answer like this or you can rewrite it as a mixed number.



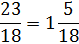
So

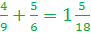
Let's Review:

To add fractions with unlike denominators, you will start by getting common denominators. Be sure to multiply the numerator by the same thing you multiply the denominator. Then add the numerators and keep the denominator the same.


Related Links:
Math
Fractions
Fraction Addition Worksheets
Convert Decimals to Fractions Quiz
Add and Subtract Like Fractions Quiz
Add and Subtract unlike fractions Quiz
Compare & Order Fractions Quiz
Multiply Fractions Quiz
Dividing Fractions Quiz
Factors