Hyperbola: Asymptotes
Let's quickly review the standard form of the hyperbola.
STANDARD EQUATION OF A HYPERBOLA:
➢ Center coordinates (h, k)
➢ a = distance from vertices to the center
➢ c = distance from foci to center
➢
transverse axis is horizontal
transverse axis is vertical
A hyperbola has two asymptotes as shown in Figure 1:
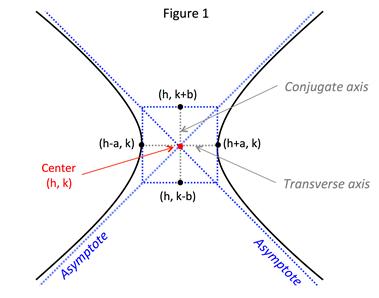
The asymptotes pass through the center of the hyperbola (h, k) and intersect the vertices of a rectangle with side lengths of 2a and 2b. The line segment of length 2b joining points (h,k + b) and (h,k - b) is called the conjugate axis.
The equations of the asymptotes are:
EQUATION OF THE ASYMPTOTES OF A HYPERBOLA:
➢ Center coordinates (h, k)
➢ a = distance from vertices to the center
➢ c = distance from foci to center
➢
transverse axis is horizontal
transverse axis is vertical
Let's use these equations in some examples:
3x2 - 2y2 + 18x + 15 = 0.
|
Step 1: Group the x- and y-terms on the left-hand side of the equation. |
3x2 - 2y2 + 18x + 15 = 0
|
|
Step 2: Move the constant term to the right-hand side. |
|
|
Step 3: Complete the square for the x- and y-groups. |
Complete the square for the x-group (3x2 + 18x) Factor out a 3 so the x2-coefficient is 1 3(x2 + 6x) Take the coefficient of the x-term, divide by 2 and square the result.
Add the result to the x-group. 3(x2 + 6x + 9) Complete the square for the y-group -2y2 Because there is no y-term no work is necessary. Final result.
|
|
Step 4: Add the values added to the left-hand side to the right-hand side. |
|
|
Step 5: Write the x-group and y-group as perfect squares. |
|
|
Step 6: Divide both sides by the value on the right-hand side, simplify and write the denominators as perfect squares. |
Divide by 12:
Write denominators as perfect squares:
|
|
Step 7: Identify h, k, a and b and the orientation of the transverse axis from the standard equation in Step 6. |
Center: (h, k) = (-3, 0) Note that x + 3 = x - (-3) a = 2
The transverse axis is horizontal since x is in the numerator above a2. |
|
Step 8: Write the equations of the asymptotes |
Equation for a horizontal transverse axis:
Substitute:
Simplify:
|
|
Step 1: Find the center coordinates. |
Center: The center is the midpoint of the two vertices.
|
|
Step 2: Determine the orientation of the transverse axis and the distance between the center and the vertices (a). |
Orientation of the transverse axis: Since both vertices fall on the vertical line x = 4, the transverse axis is vertical. Length of a: To find the length between the center and the vertices take either vertices and find the change in their y-coordinates. Vertex (4, 3): Vertex (4, 9): a = 3 |
|
Step 3: Determine the value of b. |
The given asymptote equation, has a slope of 2. Because the transverse axis is vertical, .
|
|
Step 4: Write the standard form of the hyperbola. |
Equation for a vertical transverse axis:
Substitute:
Final equation:
|
|
Related Links: Math algebra Polar Coordinates: Coordinate Conversion Polar Equation: Conversion Between Rectangular Form Pre Calculus |
To link to this Hyperbola: Asymptotes page, copy the following code to your site:
