There are many special relationships that can be formed using angles.

Here is a look at two of the relationships.

Supplementary angles are two angles that have a sum of 180°.



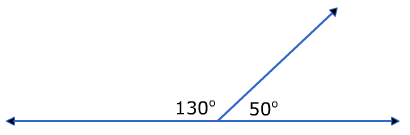
Complementary angles are two angles that have a sum of 90°.



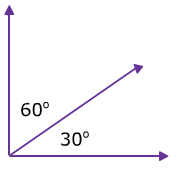
There is an easy way to try and remember these using the first letters of each word.

The S in supplementary can be used to form the 8 in 180.



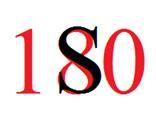
The C in complementary can be used to form the 9 in 90.



If we know that a set of angles form one of these special relationships, we can determine the measure of the other angle.

Example #1: 43°

To determine the supplement, subtract the given angle from 180.

180 - 43 = 137°   The supplement of 43° is 137°.

To determine the complement, subtract the given angle from 90.

90 - 43 = 47° The complement of 43° is 47°.

Example #2: 61°

180 - 61 = 119°   The supplement of 61° is 119°.

90 - 61 = 29° The complement of 61° is 29°.

Example #3: 127°

180 - 127 = 53° The supplement of 127° is 53°.

127° is already greater than 90°. Therefore, there is no complement.

Example #4: Determine the missing angle.



Notice that the two angles for a right angle when together. This means that the angles are complementary and have a sum of 90°.

90 - 62 = 28°

The missing angle measures 28 degrees.

Example #5: Determine the missing angle.



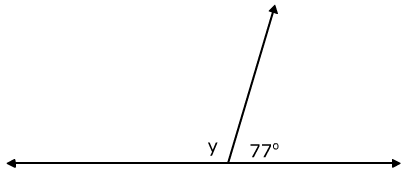
These two angles form a straight line. Straight lines measure 180°. That means that these two angles are supplementary.

180 - 77 = 103°

The missing angle measures 103 degrees.

Let's Review

Complementary angles form a right angle (L shape) and have a sum of 90 degrees.

Supplementary angles form a straight line and have a sum of 180 degrees.

If the relationship is given, you can subtract the given angle from the sum to determine the measure of the missing angle.

Related Links: Complementary and Supplementary Angle Worksheets Math Geometry Angles