Area of Triangles: Using Base and Height
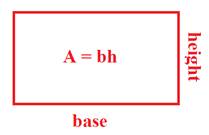
If the rectangle is cut in half, we know have a triangle. So the area would be half the area of the rectangle.
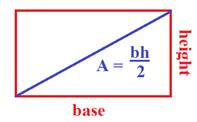
Let's use the formula in some examples.
Ex. 1) Calculate the area of the triangle.
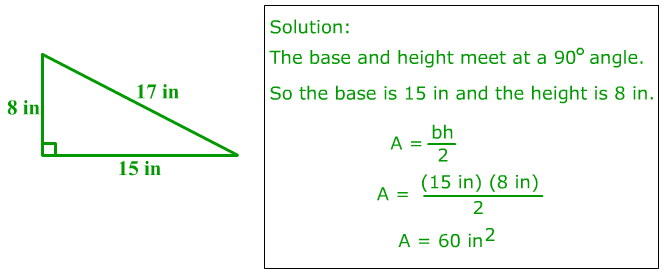
Ex. 2) Calculate the area of the triangle.

Ex. 3) Determine the area of the triangle.

Ex. 4) The area of the triangle is 32 cm2. Determine the height.
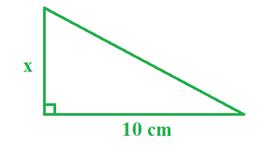
To help visualize what this problem is asking, draw the other half so that it forms a rectangle.
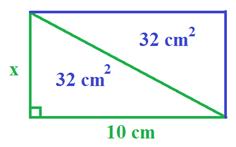
This rectangle would have an area of 64 cm2.
A = bh
64 = 10(x)
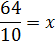
x = 6.4 cm
A = bh
64 = 10(x)
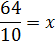
x = 6.4 cm
Let's review the steps.
Step 1: Double the area of the triangle. (This "undoes" the dividing by 2.)
Step 2: Divide the new area by the given side length.
Step 1: Double the area of the triangle. (This "undoes" the dividing by 2.)
Step 2: Divide the new area by the given side length.

Ex. 5) The area of the triangle is 40 in2. Determine the length of the height.
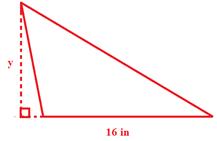
Solution:
Remember, double the area and then divide by the known side length.
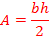
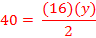
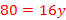
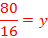
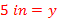

Remember, double the area and then divide by the known side length.
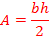
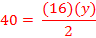
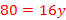
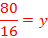
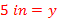

Let's Review
To calculate the area of a triangle, we multiply the base times the height and divide by 2. If you are given the area, follow the steps backwards. You will multiply by 2 and divide by the given length.
|
Related Links: Area of a Triangle Worksheets Math Geometry Triangles Geometry Practice Test: Types of Triangles Area of Triangle Perimeter of the Triangle |
