Area of a Triangle - Heron's Formula
So what do you do if you only know the three side lengths?
There are just two steps.
Step 1: Calculate half the perimeter of the triangle and call it s. 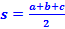
Step 2: Use the s in the following formula: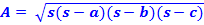
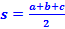
Step 2: Use the s in the following formula:
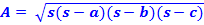

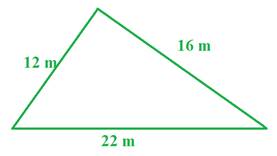
Let's use the formula to determine the area of the triangle above.
Step 1: The perimeter of the triangle is equal to 12 + 22 + 16 = 50
Therefore, the s value is half of 50 or 25.
Step 2: Replace the s in the area formula with 25 and solve.
A =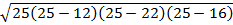
A =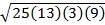
A =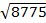
A = 93.7 m2
Therefore, the s value is half of 50 or 25.
Step 2: Replace the s in the area formula with 25 and solve.
A =
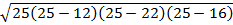
A =
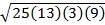
A =
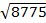
A = 93.7 m2
Here are a couple more example to try.
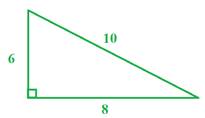
Example 1:
Step 1: Determine half the perimeter.
s = 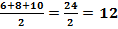
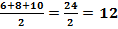
Step 2: Use the s in Heron's formula.
A = 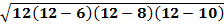
A =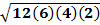
A =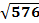
A = 24 units2
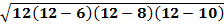
A =
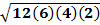
A =
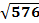
A = 24 units2
Now, this triangle does give the base and height. So let's compare our work to the formula you might be more familiar with using to solve.
A = 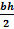
A =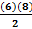
A = 24 units2
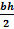
A =
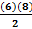
A = 24 units2
Here we have the same answer as we got from using Heron's method.
Example 2:
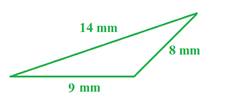
Step1: Determine half the perimeter.
Step 2: Use the s in Heron's formula.
s = 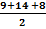
s =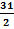
s = 15.5
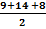
s =
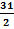
s = 15.5
Step 2: Use the s in Heron's formula.
A = 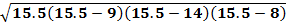
A =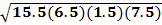
A =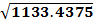
A = 33.7 mm2
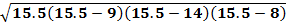
A =
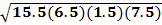
A =
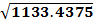
A = 33.7 mm2
When the solution is not rational, the answer can be rounded. In this example, we rounded to the nearest tenth.
Let's Review
If you are given the three sides of a triangle, you can use the perimeter and Heron's formula to determine the area. There are just two steps.
Step 1: Determine half the perimeter.
Step 2: Use the three side lengths and the half perimeter in Heron's formula.
Some of the areas will be irrational numbers. That means that they cannot be represented as a fraction. Instead they are decimals that never end and never repeat. When this happens, the area can be rounded to whatever place value you may have been asked for.
|
Related Links: Math Geometry Triangles Geometry Practice Test: Types of Triangles Area of Triangle Perimeter of the Triangle Area of a Triangle Worksheets |
