Polar Form of a Complex Number

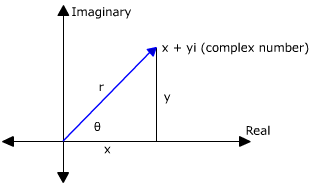
Polar form of a complex number combines geometry and trigonometry to write complex numbers in terms of distance from the origin and the angle from the positive horizontal axis. To write the polar form of a complex number start by finding the real (horizontal) and imaginary (vertical) components in terms of r and then find θ (the angle made with the real axis).

Conversion Formula for rectangular to polar x + yi = r(cos θ + i sin θ)

Example 1: convert 5 + 2i to polar form

Step 1: sketch a graph

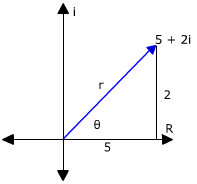
Step 2: find r using the Pythagorean Theorem

r² = x² + y²

r =

\sqrt{x^{2} + y^{2}}

r =

\sqrt{5^{2} + 2^{2}} = \sqrt{29} \approx 5.4

Step 3: Using Trigonometry find θ

Recall that tan θ = $\frac{y}{x}$ therefore tan θ = $\frac{2}{5}$

to find θ θ = $\tan^{- 1} (\frac{2}{5}) \approx 21.8 °$

Step 4: write in polar form using the conversion formula

5 + 2i = 5.4 (cos 21.8° + i sin 21.8°)

Example 2: convert 5 - 2i to polar form

Step 1: sketch a graph

Step 2: find r using the Pythagorean Theorem

r² = x² + y²

r =

\sqrt{x^{2} + y^{2}}

r =

\sqrt{5^{2} + {(- 2)}^{2}} = \sqrt{29} \approx 5.4

Step 3: Using Trigonometry find θ

Because the complex number is in Quadrant IV and θ is the angle from the positive horizontal axis to the vector: θ = 360° - β

Recall that tan β = $\frac{y}{x}$ therefore tan β = $\frac{2}{5}$

to find β β = $\tan^{- 1} (\frac{2}{5}) \approx 21.8 °$

θ = 360° - β θ = 360° - 21.8° = 338.2°

Step 4: write in polar form using the conversion formula

5 - 2i = 5.4 (cos 338.2° + i sin 338.2°)

To write a complex number in polar form: (1) draw a sketch labeling all parts (2) use the Pythagorean theorem to find the length of r (3) Find θ by using trigonometry and (4) use the formula to write in polar form.

To link to this Polar Form of a Complex Number page, copy the following code to your site:

<a href="https://www.softschools.com/math/algebra/topics/polar_form_of_a_complex_number/">Polar Form of a Complex Number</a>

Polar Form of a Complex Number

More Topics

Educational Videos