Factoring Polynomials: The difference of two squares
|
When factoring polynomials, the first step is always to look for common factors and to factor them out. After that, you can see if the polynomial can be factored further.
There is a special situation called the difference of two squares that has a special pattern for factoring. Here is the pattern: 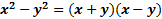 First, notice that there are three requirements that must be met in order for us to be able to use this pattern. 1) It must be a binomial (have two terms)
2) Both terms must be perfect squares (meaning that you could take the square root and they would come out evenly.) 3) There must be a subtraction/negative sign (not addition) in between them If these three requirements are met, then we can easily factor the binomial using the pattern. Simply... 1) Write two parenthesis 2) Put a  in one and a in one and a  in the othe in the othe3) Take the square root of the first term and put that in the front of each parenthesis 4) Take the square root of the last term and put that in the back of each parenthesis As before, you can check your work by multiplying out your answer and making sure the result matches the original. Here's a couple examples:
1) 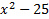 First check for common factors - there are none, so we can First check for common factors - there are none, so we can continue on to check the criteria. It is a binomial with two perfect squares and subtraction, so we can use this pattern. 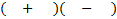 We set up two parenthesis with a+ in one and a- in the other
We set up two parenthesis with a+ in one and a- in the other 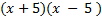 We take the square root of x2,
which is x, and put that in the We take the square root of x2,
which is x, and put that in the front of each parenthesis. We take the square root of 25 which is 5 and put that in the back of each.
Final answer: 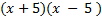 . We can check this by multiplying it out (remember to . We can check this by multiplying it out (remember to distribute or use FOIL). We get
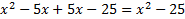 . This matches the original, so we know we factored correctly. . This matches the original, so we know we factored correctly.2) 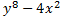 First check for common factors â there are none, so we can First check for common factors â there are none, so we can continue on to check the criteria. It is a binomial with two perfect squares and subtraction, so we can use this pattern. 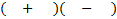 We set up two parenthesis with a+ in one and a- in the other We set up two parenthesis with a+ in one and a- in the other 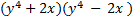 We take the square root of
We take the square root of 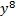 , which is , which is 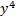 , and put that , and put that in the front of each parenthesis. We take the square root of 4x2 which is 2x and put that in the back of each. Final answer 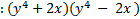 . We can check this by multiplying it out . We can check this by multiplying it out (remember to distribute or use FOIL). We get 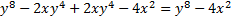 . This matches the original, so we know we factored correctly. . This matches the original, so we know we factored correctly.3) 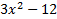 First we check for common factors. There is a common factor of 3, so we must factor that out first. First we check for common factors. There is a common factor of 3, so we must factor that out first.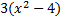 Now we look at Now we look at 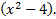 . This meets the criteria for the pattern, so we can factor it using the pattern. Just bring down the 3 in front of the parenthesis. . This meets the criteria for the pattern, so we can factor it using the pattern. Just bring down the 3 in front of the parenthesis.Answer: 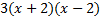 We can check this by multiplying everything out. Let's distribute the 3 first: 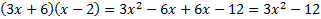 Practice: Factor the following. Check for common factors first then the difference of two squares. 1) 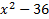 2) 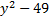 3) 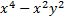 4) 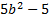 5) 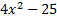 Answers: 1) 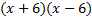 2)
2) 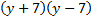 3)
3) 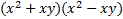 4)
4) 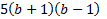 5)
5) 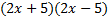
|
|
Related Links: Math Algebra Factors Polynomials Algebra Topics |
