Factoring Polynomials: Common Factors
|
Factoring can be thought of in two ways: 1) Un-multiplying. For example, 20 = 2.2.5. When we factored 20, we un-multiplied it to look like it did before it was multiplied. 2) Reverse of distribution. The distributive property says a(b + c) = ab + ac.To factor (or un-multiply) this, we would reverse the distribution.So ab + ac = a(b + c) Let's look at this in more details: 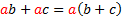 Notice that there was an Notice that there was an  in both terms of the original. When we reversed the distribution, we put the common factor in both terms of the original. When we reversed the distribution, we put the common factor  on the outside of the parenthesis and wrote in parenthesis everything that was left. on the outside of the parenthesis and wrote in parenthesis everything that was left.Let's look for common factors in the following polynomials and factor them out: 1) 3x + 3y.The common factor in this one is pretty obvious. Do you see it? 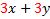 Of course 3 is our common factor because it is in both terms. Of course 3 is our common factor because it is in both terms.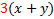 We write out common factor (3) on the outside of the parenthesis We write out common factor (3) on the outside of the parenthesis and everything else inside parenthesis. Final answer: 3(x + y) We can check our answer by distributing. :3(x + y) = 3x + 3y (the original problem) so we know we are correct. 2) 5x + 2xy. Do you see the common factor(s)? 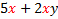 Of course x is our common factor because it is in both terms. Of course x is our common factor because it is in both terms.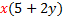 We write out common factor (x) on the outside of the parenthesis and everything else inside parenthesis. We write out common factor (x) on the outside of the parenthesis and everything else inside parenthesis. Final answer x(5 + 2y) We can check our answer by distributing. : x(5 + 2y) = 5x + 2xy (the original problem) so we know we are correct. 3) 6x + 12. The common factor isn't as obvious in this one, so we will factor first. 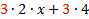 We can see that 3 is our common factor because it is in both terms. We can see that 3 is our common factor because it is in both terms.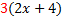 We write out common factor (3) on the outside of the parenthesis and everything else inside parenthesis, recombining the leftover factors (2 . x = 2x) We write out common factor (3) on the outside of the parenthesis and everything else inside parenthesis, recombining the leftover factors (2 . x = 2x)Final answer 3(2x + 4) We can check our answer by distributing. : 3(2x + 4) = 6x + 12 (the original problem) so we know we are correct. 4)5x2+10x. The common factor isn't as obvious in this one, so we will factor first. 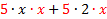 We can see that both 5 and x are our common factors We can see that both 5 and x are our common factors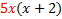 We write out common factors (5x) on the outside of the parenthesis and everything else inside parenthesis. We write out common factors (5x) on the outside of the parenthesis and everything else inside parenthesis.Final answer:5x (x + 2) We can check our answer by distributing. : 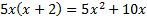 (the original (the original problem) so we know we are correct.
5) 7x + 7. The common factor is pretty obvious here. 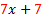 Of course 7 is our common factor because it is in both terms. Of course 7 is our common factor because it is in both terms.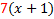 We write out common factor (7) on the outside of the parenthesis. Notice that when all the factors are removed from a term, there is still an understood 1.
Remember that factoring is reversing multiplication. We need to be able to multiply 7(x + 1) and get back to our original answer. Without the 1,we would not get back to 7x + 7 We write out common factor (7) on the outside of the parenthesis. Notice that when all the factors are removed from a term, there is still an understood 1.
Remember that factoring is reversing multiplication. We need to be able to multiply 7(x + 1) and get back to our original answer. Without the 1,we would not get back to 7x + 7Final answer 7(x + 1) We can check our answer by distributing. : 7(x + 1) = 7x + 7 (the original problem) so we know we are correct. 6)
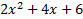 The common factor isn't perfectly clear, so we will factor first. The common factor isn't perfectly clear, so we will factor first. 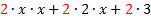 The only factor that is in all three terms is 2.x is not a common factor because it is not in the last term. The only factor that is in all three terms is 2.x is not a common factor because it is not in the last term.
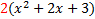 We write out common factor (2) on the outside of the parenthesis and everything else inside parenthesis, recombining the leftover factors. We write out common factor (2) on the outside of the parenthesis and everything else inside parenthesis, recombining the leftover factors. Final answer: 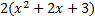 We can check our answer by distributing. : 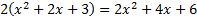 (the original (the original problem) so we know we are correct. Practice: 1) 4x + 4y 2) 6a + 9b 3) x2 - 8x 4) 10x + 2 5) 2y2 - 6y + 8 6) 8x2 + 10xy Answers: 1) 4(x + y) 2) 3(2a + 3b) 3) x(x - 8) 4) 2(5x + 1) 5) 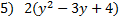 6) 2x(4x + 5y)
6) 2x(4x + 5y)
|
