Unit Vector Formula

Vectors have both a magnitude (value) and a direction. Vectors are labeled with an arrow, for example: 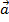. A unit vector is a vector that has a magnitude of 1. They are labeled with a "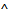", for example: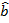. Any vector can become a unit vector by dividing it by the vector's magnitude. Vectors are often written in xyz coordinates. This can be done in two ways. One is to write the coordinates in brackets: 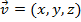. The other is to use three unit vectors, with each pointing along one of the axes: . The magnitude of a vector is:.

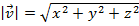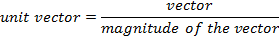
In bracket format:

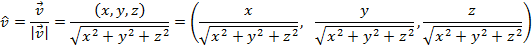
In unit vector component format:

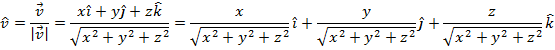
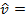= a unit vector, with direction and a magnitude of 1

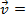= a vector, with any magnitude and direction

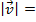= the magnitude of the vector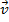

x=the value of the vector in the x axis

y=the value of the vector in the y axis

z=the value of the vector in the z axis

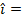= a unit vector directed along the positive x axis

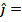= a unit vector directed along the positive y axis

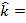= a unit vector directed along the positive z axis

Unit Vector Formula Questions:

1) Given a vector 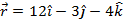, find the unit vector 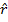. Express it in both bracket format and unit vector component format.

Answer: The magnitude of the vector 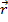is:

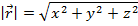
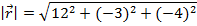
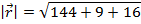
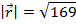
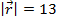
The magnitude can now be used to find the unit vector :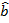

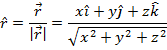
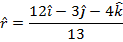
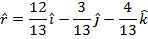
In bracket format, the unit vector is:

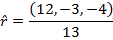
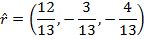
Since the answer was not asked for using decimal numbers, leaving the numbers in the vector as fractions is best.

2) Given a vector 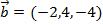, find the unit vector 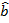. Express it in both bracket format and unit vector component format.

Answer: The magnitude of the vector 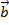is:

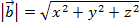
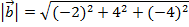
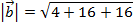
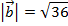
The magnitude can now be used to find the unit vector :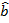

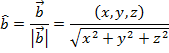
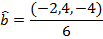
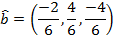
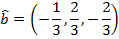
In unit vector component format, the unit vector is:

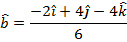
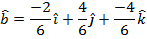
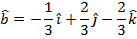
Since the answer was not asked for using decimal numbers, leaving the numbers in the vector as reduced fractions is best.