Parallel Axis Theorem Formula
The moment of inertia is a value that measures how difficult it is to change the state of an object's rotation. The same object can have different moments of inertia, depending where the rotational axis is. If the moment of inertia for an axis through an object's center of mass is known, it is possible to find the value of the moment of inertia for any other parallel axis. This is called the parallel axis theorem. The unit for moment of inertia is the kilogram-meter squared, 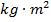 .
.
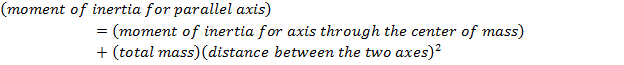
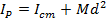
Ip = moment of inertia for rotation around a parallel axis (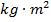 )
)
Icm = moment of inertia for rotation around an axis through the center of mass (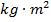 )
)
M = total mass of the object (kg)
d = distance between the two rotation axes (m)
Parallel Axis Theorem Formula Questions:
1) A solid sphere with mass 60.0 kg and radius 0.150 m has a moment of inertia 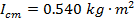 for rotation through its central axis. What will be the moment of inertia of the sphere, if the rotation axis is changed to pass through a point on its surface?
for rotation through its central axis. What will be the moment of inertia of the sphere, if the rotation axis is changed to pass through a point on its surface?
Answer: If the rotation axis is changed from the center axis of the sphere to an axis that connects to the surface of the sphere, then the distance between these points is the radius of the sphere: d = 0.150 m. The mass and moment of inertia through the sphere's center of mass are given. Using these, the moment of inertia for the parallel axis can be calculated using the formula:
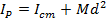
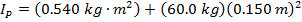
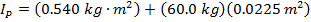
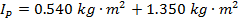
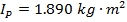
The moment of inertia for rotation around the axis at the surface of the sphere is 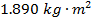 .
.
2) A long rod with mass has a moment of inertia 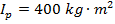 , for rotation around an axis near one end. The total length of the rod is 10.00 m. What is the moment of inertia for rotation through the rod's center?
, for rotation around an axis near one end. The total length of the rod is 10.00 m. What is the moment of inertia for rotation through the rod's center?
Answer: If the full length of the rod is 10.00 m, then the distance between one end of the rod and the center is 5.00 m. The mass and moment of inertia through a parallel axis are given. Using these, the moment of inertia for the central axis parallel axis can be found by rearranging the parallel axis theorem formula:
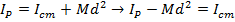
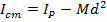
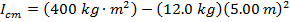
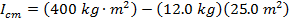
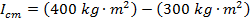
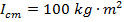
The moment of inertia for rotation through the center of the rod is 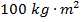 .
.
|
Related Links: |
