Orbital Velocity Formula

Objects that travel in uniform circular motion around the Earth are said to be "in orbit". The velocity of this orbit depends on the distance from the object to the center of the Earth. The velocity has to be just right, so that the distance to the center of the Earth is always the same.The orbital velocity formula contains a constant, G, which is called the "universal gravitational constant". Its value is = 6.673 x 10^-11 N∙m²/kg² .The radius of the Earth is 6.38 x 10⁶ m.

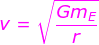
v = the orbital velocity of an object (m/s)

G = the universal gravitational constant, G = 6.673x10^(-11) N∙m²/kg²

m_E = the mass of the Earth (5.98 x 10²⁴ kg)

r = the distance from the object to the center of the Earth

Orbital Velocity Formula Questions:

1) The International Space Station orbits at an altitude of 400 km above the surface of the Earth. What is the space station's orbital velocity?

Answer: The orbital velocity depends on the distance from the center of mass of the Earth to the space station. This distance is the sum of the radius of the Earth and the distance from the space station to the surface:

r = (6.38 x 10⁶ m) + (400 km)

r = 6380000 + 400000 m

r = 6780000 m

The orbital velocity can be found using the formula:

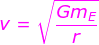
v=7672 m/s

The orbital velocity of the International Space Station is 7672 m/s.

2) A satellite is orbiting the Earth with an orbital velocity of 3200 m/s. What is the orbital radius?

Answer: The orbital radius can be found by rearranging the orbital velocity formula:

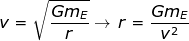
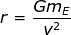
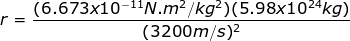
The orbital radius for this satellite is 3.897 x 10⁷ m.