One-Dimensional Kinematics Formula

One-dimensional motion can be described using formulas that relate displacement, velocity, and acceleration. Velocity is the rate of change of displacement with respect to time. Acceleration is the rate of change of velocity with respect to time. In these formulas, the acceleration is assumed to be constant. The unit of displacement is the meter (m), the unit of velocity is meters per second (m/s), and the unit of acceleration is meters per second squared (m/s²).

Velocity

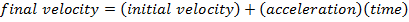
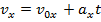
Displacement

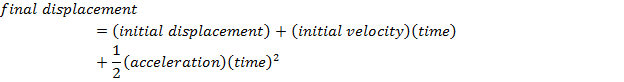
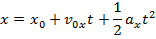
Velocity, Acceleration, Displacement

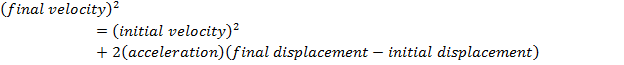
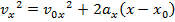
Displacement and Velocity

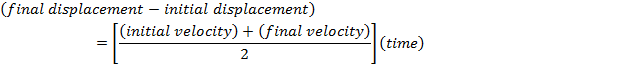
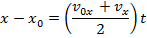
x₀ = initial displacement (m)

x = final displacement (m)

v_0x = initial velocity (m/s)

v_x = final velocity (m/s)

a_x = acceleration (m/s²)

t = time (s)

One-Dimensional Kinematics Formulas Questions:

1) A running cheetah begins accelerating as it passes a tree, and runs a distance of 60.0 m in 5.00 s. As the cheetah passes this second point, its speed is 15.0 m/s. What was the speed of the cheetah when it passed the tree (when it began accelerating)?

Answer: The first steps in a one-dimensional kinematics problem are to identify what values are known, and then determine which formula will be the most helpful. In this problem, the distance traveled is known, which provides an initial and final position: x₀ = 0.0 m, and x = 60.0 m. The final velocity is given: v_x = 15.0 m/s. Finally, the time for which the cheetah accelerates is given: t = 5.00 s. The value asked for in the question is the initial velocity: v_0x. The cheetah's acceleration is not given, and so the best formula is the one that does not include it:

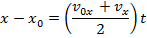
The cheetah's initial velocity can be found by rearranging this formula:

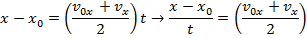
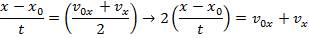
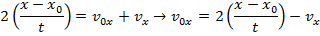
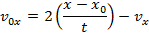
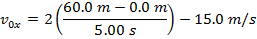
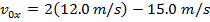
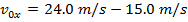
v_0x = 9.0 m/s

The cheetah's initial velocity was 9.0 m/s.

2) A toy rocket blasts off from the ground with an initial velocity of 18.0 m/s. Ignoring air resistance, what is the maximum height reached by the rocket before it begins falling?

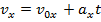
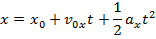
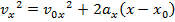
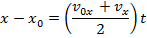
Answer: The first steps in a one-dimensional kinematics problem are to identify what values are known, and then determine which formula will be the most helpful. In this problem, the initial position can be assigned the value x₀ = 0.0 m, though the final position x is unknown, and asked for in the problem. The initial velocity of the rocket is v_0x = 18.0 m/s. At the rocket's maximum height, it will reverse direction. At this point, the rocket's velocity will be zero: v_x = 0.0 m/s. The constant acceleration that the rocket experiences is due to gravity. The acceleration due to gravity is directed downward, and so in this problem, it will have a negative direction: 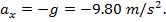The amount of time the rocket takes to reach its maximum position is not known, and so the best formula is the one that does not include time t:

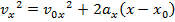
The toy rocket's maximum height can be found by rearranging this formula:

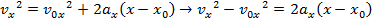
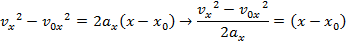
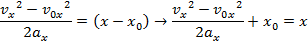
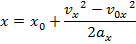
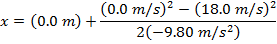
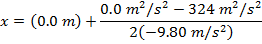
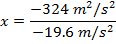
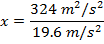
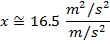
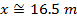
The maximum height reached by the toy rocket is 16.5 m.