Kirchhoff's Loop Rule Formula

In any "loop" of a closed circuit, there can be any number of circuit elements, such as batteries and resistors. The sum of the voltage differences across all of these circuit elements must be zero. This is known as Kirchhoff's Loop Rule. Voltage differences are measured in Volts (V). When the current I in the loop is given in Amperes (A) and resistance of circuit elements is given in Ohms (Ω), the voltage difference across a resistor can be found using the formula .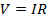

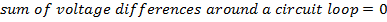
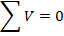
V = voltage difference, (Volts, V)

Kirchhoff's Loop Rule Formula Questions:

1) The circuit loop in the figure below consists of three resistors and a voltage source (battery). The current in the loop is I = +4.00 A, clockwise. The battery supplies a voltage of v_b = 100.0 V. The resistance values for two of the three resistors are given in the figure. What is the value of resistor R₃ ?

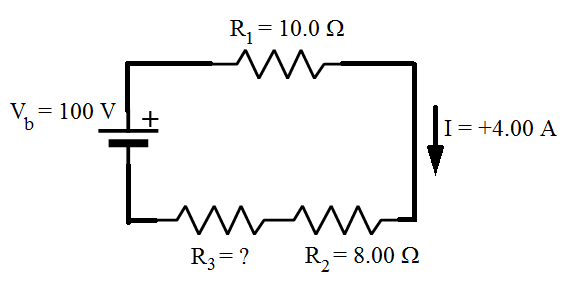
Answer: Kirchhoff's Loop Rule states that the sum of the voltage differences around the loop must be equal to zero. To find the sum, a direction of travel must be chosen. The direction of positive current is given as clockwise, and so it is easiest to use this as the direction of travel to find the sum. The voltage source, or battery, on the left in the figure has a positive voltage value in the clockwise direction. The three resistors cause voltage drops in this direction. The magnitude of the voltage drops are equal to the resistance multiplied by the current in the loop. The sum of the voltage differences is:

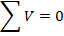
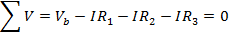
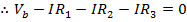
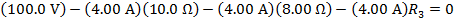
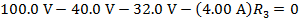
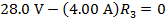
The value of the third resistor can be found by rearranging the formula above:

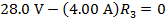
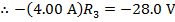
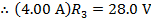
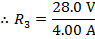
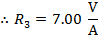
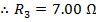
The value of resistor R₃ is 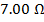(Ohms).

2) The circuit loop in the figure below consists of three resistors and a voltage source (battery). The current in the loop is I = +10.0 mA(milli-Amperes), counter-clockwise. The values for the three resistors are given in the figure, in units of kilo-Ohms (The value of resistor R₃ is 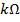). What voltage (V_b) must be supplied by the battery?

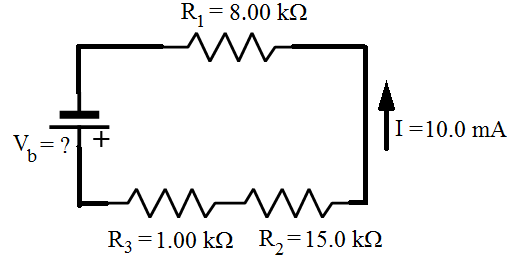
Answer: Kirchhoff's Loop Rule states that the sum of the voltage differences around the loop must be equal to zero. To find the sum, a direction of travel must be chosen. The direction of positive current is given as counter-clockwise, and so it is easiest to use this as the direction of travel to find the sum. The voltage source, or battery, on the left in the figure has a positive voltage value in the counter-clockwise direction. The three resistors cause voltage drops in this direction. The magnitude of the voltage drops are equal to the resistance multiplied by the current in the loop, and so the total of these must be of the same magnitude as the voltage from the battery. The sum of the voltage differences, in the chosen direction of travel is:

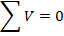
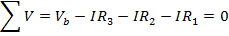
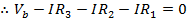
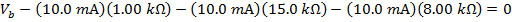
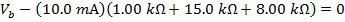
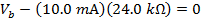
To multiply the values in the above formula, the current and resistance values have to be converted to the base units. For current, 1000 milli-Amperes equal 1 Ampere (1000 mA = 1 A), and for resistance,1 kilo-Ohm equals 1000 Ohms (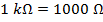). The formula becomes:

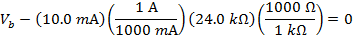
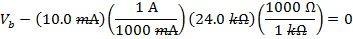
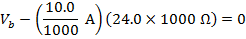
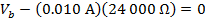
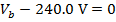
The voltage from the battery can be found by rearranging the formula above:

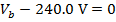
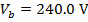
The voltage supplied by the battery V_b is 240 V(Volts).