Instantaneous Speed Formula

Speed is the rate of change of position with time. The speed of an object can change as it moves. The instantaneous speed is the speed of an object at a certain instant of time. If the position is a function of time, then the speed depends on the change in the position as time changes. The instantaneous speed can be found as this change in time becomes small. Calculating the instantaneous speed requires finding the limit of the position function as the change in time approaches zero. Speed is a scalar quantity, meaning that it has a magnitude (a value), but no direction. For that reason, speed can never be negative. The unit for speed is meters per second (m/s).

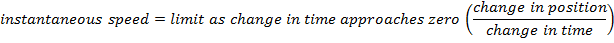
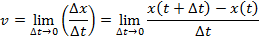
v = instantaneous speed (m/s)

Δ = "the change in", represented with the Greek letter "delta" (unitless)

x(t) = position as a function of time (m)

t = time (s)

Instantaneous Speed Formula Questions:

1) When an object is dropped and acted on by gravity, its position changes according to the function x(t) = 4.9t², and x(t) is in units of meters. What is the instantaneous speed at t = 5.0 s?

Answer: The instantaneous speed can be found using the formula:

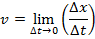
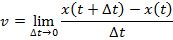
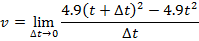
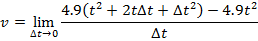
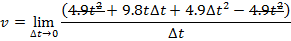
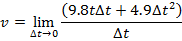
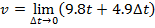
v = 9.8t

v = 9.8(5.0) m/s

v = 49.0 m/s

The instantaneous speed at t = 5.0 s is 49.0 m/s.

2) A car stops at a traffic light, and then begins moving along a straight road. The car's distance from the light is given by the function x(t) = bt³ - ct², where the constants are b = 0.900 m/s³ and c = 2.70 m/s². What will be the instantaneous speed at t = 3.00 s?

Answer: The instantaneous speed can be found using the formula:

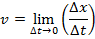
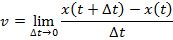
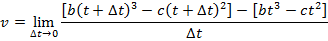
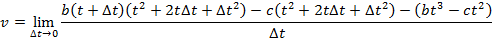
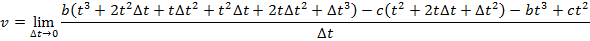
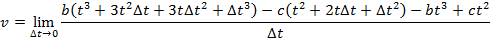
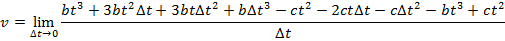
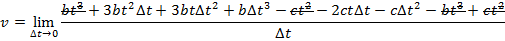
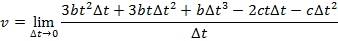
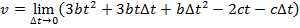
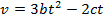
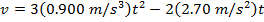
At t = 3.00 s, the instantaneous speed is:

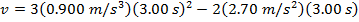
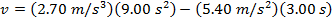
v = 24.3 m/s - 16.2 m/s

v = 8.1 m/s

The instantaneous speed of the car at t = 3.00 s is 8.1 m/s.