Hooke's Law Formula
Pulling or pushing a spring away from its equilibrium (resting) position requires a force to be applied. When the spring is held at a distance x from its equilibrium position, the spring exerts a restoring force in the negative x direction. For many springs, the restoring force is proportional to the distance away from equilibrium the spring is held. This is known as Hooke's Law. The relationship between the force and the distance is determined by a constant. The spring constant k is specific to a certain spring, and has units Newtons per meter (N/m). The unit of the restoring force is Newtons (N).
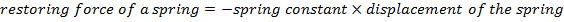
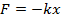
F = restoring force of a spring (Newtons, N)
k = spring constant (N/m)
x = displacement of the spring (m)
Hooke's Law Formula Questions:
1) A long, slinky spring has a spring constant of 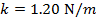 . If the spring is stretched 1.50 m, what is the restoring force exerted by the spring?
. If the spring is stretched 1.50 m, what is the restoring force exerted by the spring?
Answer: The restoring force can be found using the formula for Hooke's Law:
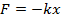
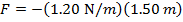
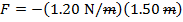
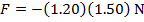
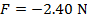
The restoring force of the spring is -2.40 N (Newtons). This means the force has a magnitude of 2.40 N, and is directed toward the equilibrium position.
2) A tough, shock-absorbing spring has been compressed a distance of 1.00 cm by exerting a force of 1500 N on the spring. What is the force constant k for this spring?
Answer: The force exerted on the spring has a magnitude of 1500 N. This means that the spring is exerting an equal (magnitude) and opposite (sign) restoring force of -1500 N. The spring is compressed a distance of 1.00 cm. To find the spring constant in units of N/m, the distance must be converted to meters:
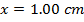
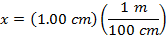
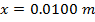
The force constant can be found by rearranging for the formula for Hooke's Law:
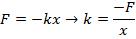
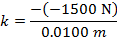
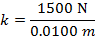
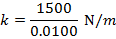
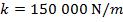
The spring constant of the shock-absorbing spring is 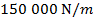 .
.
|
Related Links: |
