Decibel Formula

The intensity of a sound wave is the rate at which it transports energy per unit area. This is equivalent to average power per unit area, expressed as Watts per square meter (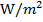). A more common way to express sound intensity is using the decibel scale. The decibel scale uses the logarithmic function to represent a large range of intensities easily. The unit of the scale is the decibel, dB.

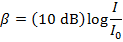
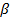= sound intensity, in decibels (dB)

I = sound intensity ()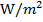

I₀ = reference sound intensity ()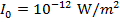

Decibel Formula Questions:

1) The sound intensity inside a car is 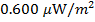. What is this sound intensity in decibels?

Answer: The sound intensity in the car is expressed in micro-Watts per meter squared. The first step is to convert this to 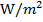. "Micro" means 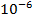, and so the sound intensity in the car is:

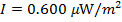
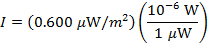
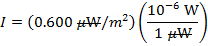
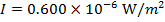
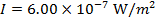
The intensity of the sound in decibels can now be found using the decibel formula:

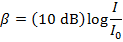
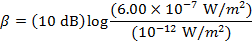
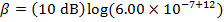
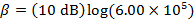
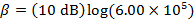
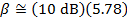
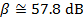
The sound intensity in the car is approximately 57.8 dB.

2) A worker uses double ear protection, both earplugs and earmuffs, to reduce the intensity of the sound of a jackhammer. This reduces the intensity of the sound he hears from 120 dB to 85.0 dB. What is the ratio of the full sound intensity to the reduced sound intensity the worker hears?

Answer: The decibel scale is logarithmic, and so a small drop in the decibel intensity means a much larger drop in the intensity expressed as 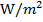. This problem can be solved by finding I for decibel values of 120 dB and 85.0 dB, and then dividing the full intensity by the reduced intensity. The mathematical formula for logarithms needed is:

If 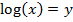, then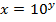

Using this mathematical formula for logarithms, the decibel formula can be rearranged to solve for I:

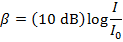
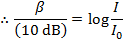
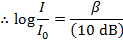
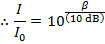
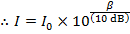
To identify which sound is which, they can be labeled with the index values 1 and 2:

,

,

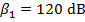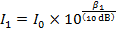
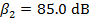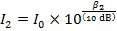
The ratio of the full sound intensity to the reduced sound intensity, expressed as Watts per meter squared is 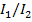. Therefore, this ratio is:

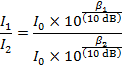
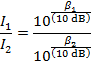
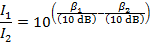
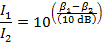
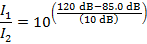
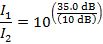
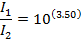
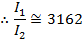
The ratio of the full sound intensity to the reduced sound intensity the worker hears is approximately 3162. Therefore, by putting on both layers of ear protection, the worker reduces the sound intensity by a factor of 3162.

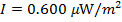
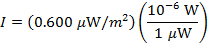
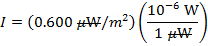
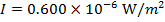
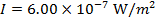
The intensity of the sound in decibels can now be found using the decibel formula:

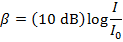
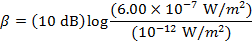
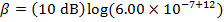
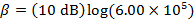
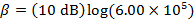
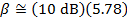
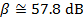
The sound intensity in the car is 57.8 dB.