Centripetal Acceleration Formula

When an object moves along a circular path, the direction of the object's velocity must constantly change. A changing velocity means that there must be an acceleration. This acceleration is perpendicular to the direction of the velocity. This is called the radial acceleration, or centripetal acceleration ("centripetal" means "center seeking"). The radial acceleration is equal to the square of the velocity, divided by the radius of the circular path of the object. The unit of the centripetal acceleration is meters per second squared ().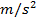

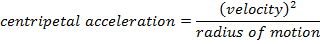
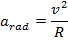
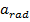= radial, or centripetal, acceleration (m/s²)

v = velocity (m/s)

r = radius of motion of the object (m)

Centripetal Acceleration Formula Questions:

1) A certain ride at an amusement park includes a circle of radius 3.00 m, that spins the riders at a velocity of 6.00 m/s. What is the centripetal acceleration of a rider?

Answer: The centripetal acceleration of a rider can be found using the formula:

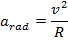
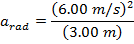
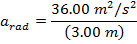
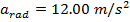
The centripetal acceleration of a rider on the carnival ride is 12.00 m/s².

2) A driver of a racing car has practiced on a certain curve of a track until she knows how fast she is able to drive without skidding. At a velocity of 45.0 m/s, the "lateral acceleration sensor" in her car reads 0.92g, meaning her centripetal acceleration is 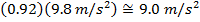. What is the radius of the curve?

Answer: The radius of the curve can be found by re-arranging the centripetal acceleration formula:

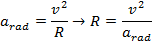
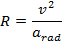
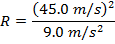
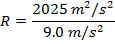
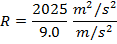
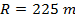
The radius of the curve in the race track is 225 m.