Capacitors in Series Formula

In electric circuits, it is often possible to replace a group of capacitors with a single, equivalent capacitor. The equivalent capacitance of a number of capacitors in series can be found using the reciprocal of capacitance, 1/C. The reciprocal of the equivalent capacitance is equal to the sum of the reciprocals of each capacitance. The unit of capacitance is the Farad (F), which is equal to a Coulomb per Volt (1 F = 1 C/V), though most electronic circuits use much smaller capacitors. Picofarad (1 pF = 10^-12 F), nanofarad (1 nF = 10^-9 F), and microfarad (1 µF = 10^-6 F) capacitors are common.

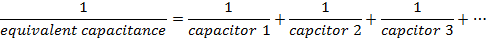
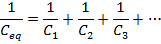
C_eq = equivalent capacitance (F or smaller units)

C₁ = capacitance of first capacitor (F)

C₂ = capacitance of second capacitor (F)

C₃ = capacitance of third capacitor (F)

Capacitors in Series Formula Questions:

1) What is the equivalent capacitance of a 100.0 µF and a 400.0 µF capacitor connected in series?

Answer: The capacitances are both expressed in microfarads, and so there is no need to change their units. The equivalent capacitance can be found in microfarads using the formula:

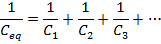
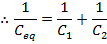
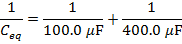
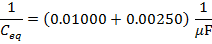
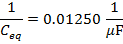
The final step is to invert the values on both sides of the formula to find the equivalent capacitance:

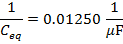
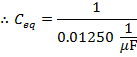
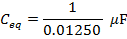
C_eq = 80.00 µF

The equivalent capacitance of the 100.0 µF and 400.0 µF capacitors in series is 80.00 µF.

2) Three capacitors are connected in series in an electric circuit. Their capacitances are 100 pF, 10.0 nF, and 1.00 µF. What is the equivalent capacitance?

Answer: The three capacitance values are expressed using different units. The first step to finding the equivalent capacitance is to convert these to a common unit. It is not necessary to convert them all to Farads. Two of the values can be converted to the same unit as the third. In this solution, all of the values will be converted to picofarads.

If C₁ = 100 pF, C₂ = 10.0 nF, and C₃ = 1.00 µF, then:

C₂ = 10.0 nF

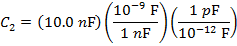
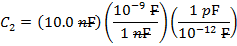
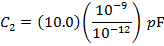
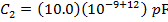
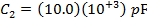
C₂ = 10 000 pF

The value of C₃ is:

C₃ = 1.00 µF

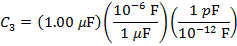
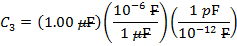
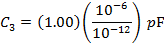
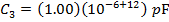
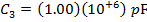
C₃ = 1 000 000 pF

The equivalent capacitance can be found in picofarads using the formula:

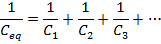
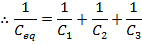
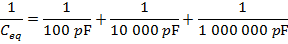
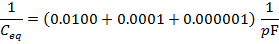
The final step is to invert the values on both sides of the formula to find the equivalent capacitance:

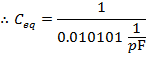
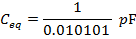
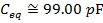
The equivalent capacitance of the 100 pF, 10.0 nF, and 1.00 µF capacitors in series is approximately 99.00 pF.