Radioactive Half-Life Formula
A radioactive half-life refers to the amount of time it takes for half of the original isotope to decay. For example, if the half-life of a 50.0 gram sample is 3 years, then in 3 years only 25 grams would remain. During the next 3 years, 12.5 grams would remain and so on.
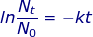
Nt = mass of radioactive material at time interval (t)
N0 = mass of the original amount of radioactive material
k = decay constant
t = time interval (t1/2 for the half-life)
Radioactive Half-Life Formula Questions:
1. If the half-life of 100.0 grams of a radioactive isotope is 8 years, how many grams will remain in 32 years?
Answer:
To answer this question, there is no need to solve for the radioactive decay equation. If 32 ÷ 8 = 4, then the material will go through 4 half-lives.
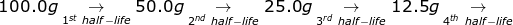 6.25g
6.25g
2. What is the decay constant for a radioactive isotope with a half-life of 22.5 hours?
At first glance, it may seem that not enough information was provided to solve this problem. However, if the half-life value is given for time (t) then the value of 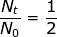 (because only half of the original material remains).
(because only half of the original material remains).
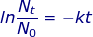
ln 0.5 = -k(22.5)
-.693 = -k(22.5)
k = 0.0308 hours-1
|
Related Links: |
